Variability Analysis of Stars

Harmonic Analysis (Asteroseismology)

To describe the variability in brightness of a variable star it is quite common that harmonic analysis is used. This harmonic analysis consists of a (iterative) Fourier decomposition of the observed signal, resulting in parameters that describe the variability using a sum-of-sines or variability model $F(t_i)$ for the observed (photometric) light curve:

\[F(t_i) = \beta_0 + \sum_{j=1}^{n_{\rm f}} A_j \sin\left[2\pi\nu_jt_i + \phi_j\right]\]

where $\beta_0$ is a parameter that corrects for a detrending offset, and the parameters with subscript $j$ relate to the variability amplitudes ($A_j$), (temporal) variability frequencies ($\nu_j = \omega_j / 2\pi$) and variability phases ($\phi_j$) at a specific time $t_i$ for which the stellar brightness was observed.

The frequencies of such variability models are then compared to the theoretically predicted oscillation frequencies of linear oscillation theory to assess which stellar structure (and evolution) models fit the observed variability best. Doing so thus allows the asteroseismologist to constrain (numerical implementations of) stellar structure and evolution models.

For additional technical details on harmonic analysis in the context of asteroseismology, I refer the interested reader towards section 2 of Van Beeck et al. (2021) or section 2.3 of my PhD thesis.

Example of a photometric light curve as observed by the NASA Kepler space telescope. — Photometric light curve of KIC6352430, a slowly pulsating B star observed by the NASA Kepler space telescope. On the y-axis you may find flux (in parts per million) relative to a baseline value, whereas on the x-axis the time coordinate is displayed in terms of Barycentric Julian dates relative to a reference date.

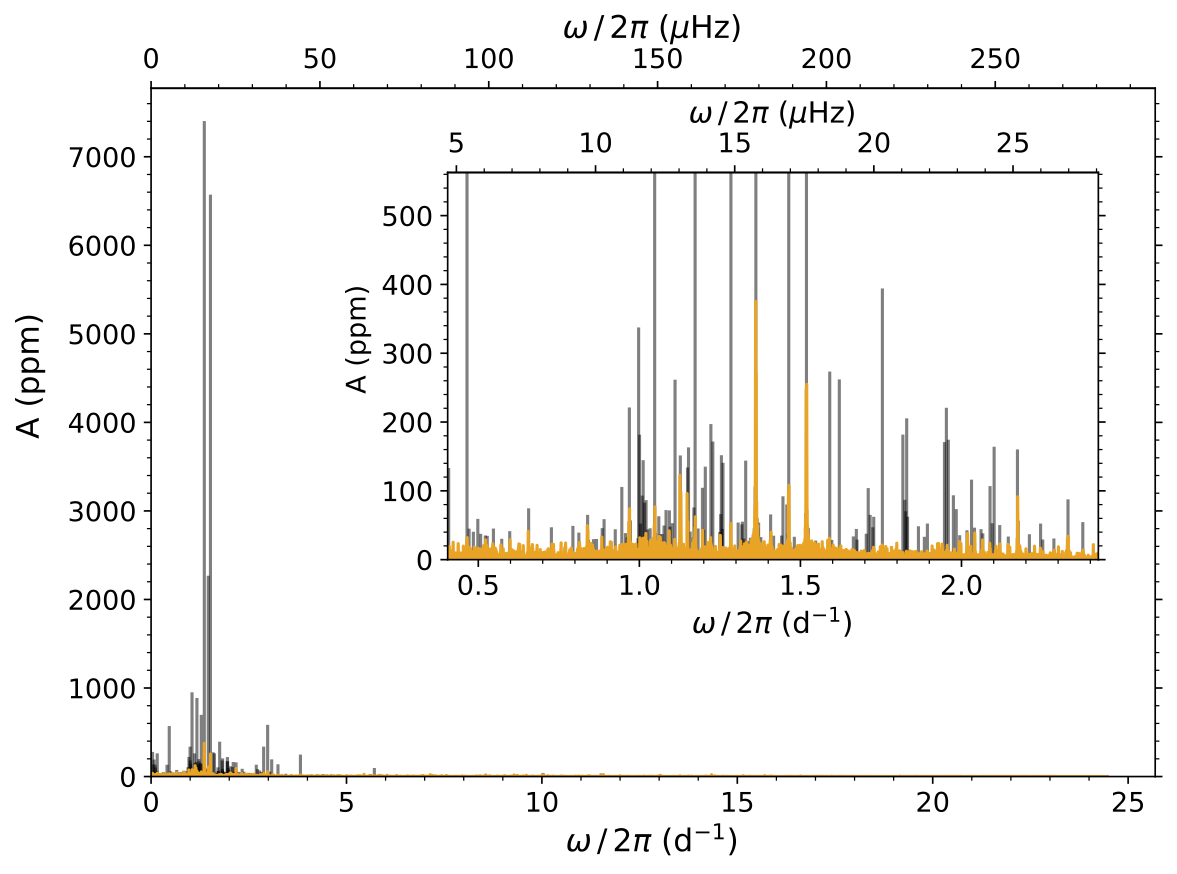
Example of a resulting amplitude spectrum of a variable star obtained by Fourier Analysis. — Fourier amplitude spectrum of KIC6352430, a slowly pulsating B star observed by the NASA Kepler space telescope. On the y-axis the variability amplitudes are displayed in parts per million, whereas the x-axis shows the (temporal) variability frequencies. In grey we show the Fourier amplitude spectrum of the original light curve, whereas the orange spectrum denotes the variability of the residuals after the iterative procedure has come to an end (because a certain stopping criterion was triggered; see Van Beeck et al. 2021 and section 2.3 of my PhD thesis).

Robust Frequency Analysis

Several approaches to harmonic analysis (or iterative prewhitening) were taken in literature. One often undefined source of uncertainty when performing such analysis is the lack of assessment of how various approaches systematically influence results.

We employed five different strategies that emulate various approaches taken in literature and assessed their capacity for modeling the light curves. This resulted in robust variability models (that take into account systematics) for a sample of slowly pulsating B stars observed by the NASA Kepler space telescope in Van Beeck et al. (2021). Other works have used the same computational framework to characterize variability in the light curves of close ellipsing binaries with tidally perturbed gravity-mode oscillations, HD 112429 (where it was used to measure near-core rotation), and identified g-mode pulsators of the young open cluster UBC1 (to age-date the cluster).

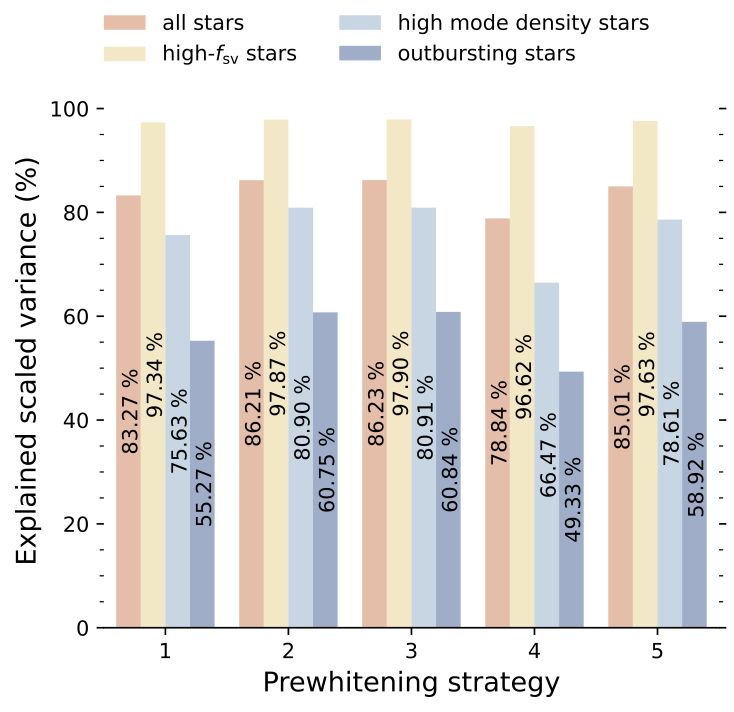
Explained Scaled Variances obtained by analyzing a sample of SPB stars using the 5 strategies embedded in NTSA. — Percentage of explained scaled variance of the light curves of a sample of slowly pulsating B (SPB) stars that was subjected to 5 different harmonic analysis/prewhitening procedures. A further subdivision of the SPB stars was made based on features in their Fourier amplitude spectra (see Van Beeck et al. 2021 and chapter 2 of my PhD thesis for details).

Resonant Frequency Detection

Linear asteroseismology employs oscillation mode frequencies to model waves propagating in stellar interiors (and constrain the numerical implementations of physical laws included in these models of the stellar interior). It is clear however that using only the variability frequencies leaves much of the information in the variability model $F(t_i)$ unused. Linear theory also cannot explain why some oscillation modes are sustained (and observed) for long periods inside stars.

To explain why some modes are excited and others are damped - the problem of mode selection - a non-linear wave formalism is required because this model can simulate (significant, non-linear) energy exchanges/coupling between modes that might be of importance for mode excitation. The lowest-order non-linear coupling theories describe interactions between sets of 3 modes, or triads, with resonant interactions being the strongest.

One important goal of my research is to identify and characterize the parameters of resonantly interacting oscillation modes. An example of the detection of resonant triads is given in Van Beeck et al. (2021) (more specifically, check out their fourth section). I also find the construction of artificially intelligent models to detect non-linear resonances in variable stars intriguing.

Relevant Publications & Software

Software

Check out the NTSA computational framework that we developed for the purpose of robust frequency analysis and the detection of resonant frequencies. A succinct description of this software suite is given on the relevant software page.

While this framework is currently limited to harmonic analysis for analyzing variability, some (baby) steps have been taken towards extensions that can model types of non-harmonic variability. As an example of physically relevant situations in which non-harmonic variability is expected, non-linear mode coupling theories predict time-variable mode parameters of interacting modes when certain (selection) conditions are fulfilled. Other examples of such situations include various transient astronomical events (also called transients), such as different types of (super)novas or tidal disruption events (among others). It is therefore a long-term goal of mine to include functionality in the NTSA framework that can detect and characterize such non-harmonic behavior.

Publications

Van Beeck J., Bowman D. M., Pedersen M. G., Van Reeth T., Van Hoolst T., Aerts C.; Detection of non-linear resonances among gravity modes of slowly pulsating B stars: results from five iterative pre-whitening strategies. November 2021, Astronomy & Astrophysics, Vol. 655, A59. HTML PDF

Van Reeth T., Southworth J., Van Beeck J., Bowman D. M.; V456 Cyg: an eclipsing binary with tidally perturbed g-mode pulsations. March 2022, Astronomy & Astrophysics, Vol. 659, A177. HTML PDF

Van Reeth T., De Cat P., Van Beeck J., Prat V., Wright D. J., Lehmann H., Chene A.-N., Kambe E., Yang S. L. S., Gentile G., Joos M.; The near-core rotation of HD112429: A $\gamma$ Doradus star with TESS photometry and legacy spectroscopy. June 2022, Astronomy & Astrophysics, Vol. 662, A58. HTML PDF

Van Reeth T., Johnston C., Southworth J., Fuller J., Bowman D. M., Poniatowski L., Van Beeck J.; Tidally perturbed gravity-mode pulsations in a sample of close eclipsing binaries. March 2023, Astronomy & Astrophysics, Vol. 671, A121. HTML PDF

Fritzewski D. J., Van Reeth T., Aerts C., Van Beeck J., Gossage S., Li G.; Age-dating the young open cluster UBC1 with g-mode asteroseismology, gyrochronology, and isochrone fitting. January 2024, Astronomy & Astrophysics, Vol. 681, A13. HTML PDF

Jordan Van Beeck